Rep-Tileパズルの解の総数はいくつ? –論理式を用いた計数–
Rep-Tileというパズルをみなさんご存知でしょうか? いわゆるタイルの敷き詰めパズルなのですが、この記事ではそのRep-Tileを題材に敷き詰め方の総数を求める問題についてお話します。ここでは、その問題を解く1つの手段として、論理式の解の計数問題に変換して解くという、汎用の問題を解く既存のソルバを活用する方法をご紹介します。

Rep-Tileとは?
最初にRep-Tileについて説明します。まず例を挙げると、たとえば、下図の左のJの形をした図形を考えたときに、右のようにより小さいJ型の図形で敷き詰めることができます。
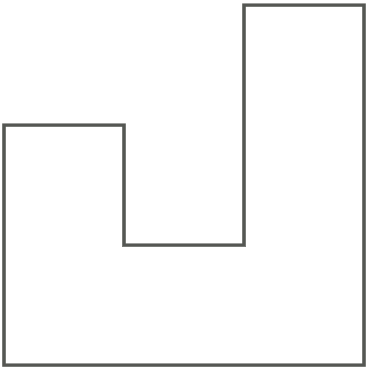
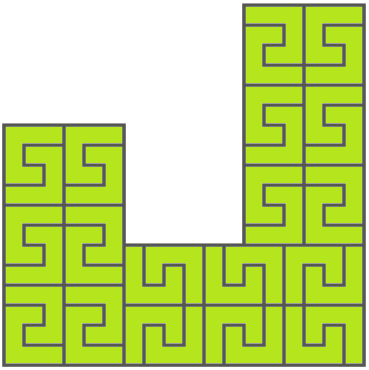
このように、自身と相似なより小さい図形で敷き詰めることができる図形のことをRep-Tileとよびます。他にも、以下のような図形もRep-Tileです。
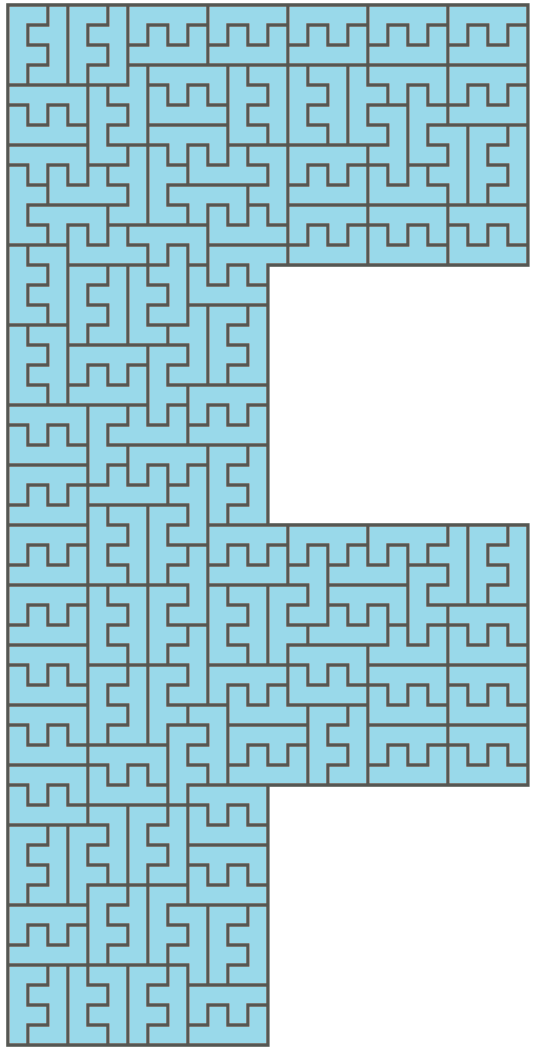
最初に挙げたJ型の例は、単位サイズのJ型タイルを6倍の相似形の領域に敷き詰めたものになっています。J型については、倍率が6の倍数である相似形のときにRep-Tileであることが証明されています。ここでは以降、J型タイルに絞って話をしていきます。
全部で何通り?
J型の6倍の相似形は単位サイズの同型タイルで敷き詰め可能であることは説明しましたが、敷き詰め方はたくさんあります。では、全部で何通りあるでしょうか?答えは262144通りです。12倍だとどうでしょうか?545409716939029673955819520通りになります。かなり大きな数ですね。
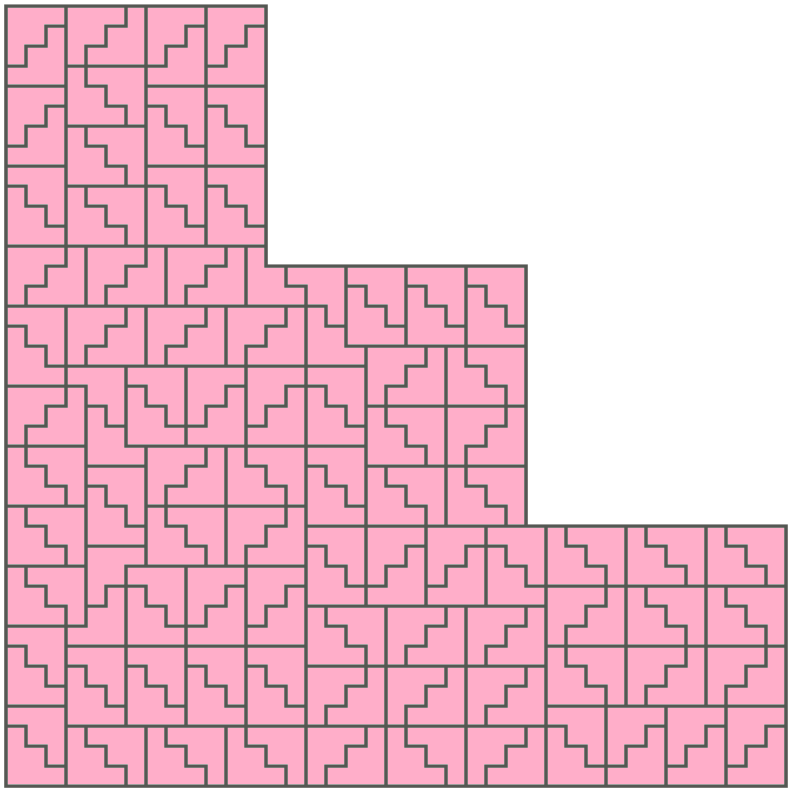
では、18倍の領域だとタイルの敷き詰め方は何通りあるでしょうか?
以下は敷き詰め方の一例です。

敷き詰め方の総数は膨大な数になりますので、1つ1つ数えていては当然いつまでたっても終わりません。また、敷き詰めていくパターンをいくつか思い付く方はいると思いますが、思い付いたもの以外のパターンが存在しないことを確認するのも結構大変です。
プログラミングができる人ならば、計算方法を頭に思い描いて、その方法をどうやってコンピュータプログラムとして書くかを考えるでしょう。パズルの特徴を考察して、パターンを網羅的に列挙できる方法を考えて、似たような計算を繰り返さないために部分的な結果を記憶・再利用していく方法を考えて、… などなど。これはこれで計算手順(アルゴリズム)を考える楽しみがありますが、一から突き詰めて考えていくとこれまた大変な作業です。
論理式に変換して解いてみる
ここでは、直接的に敷き詰め方の総数を求めるプログラムを書くのではなく、Rep-Tile問題を論理式に変換して、論理式の解の計数を行う既存のプログラム(計数ソルバ)を用いて解くというアプローチを紹介します。 Rep-Tileの解の計数問題を論理式に変換するといってもピンとこない人が多いかもしれません。後ほど変換について説明しますが、大雑把に書けば、Rep-Tile問題の並べ方が満たすべき条件を論理式の形で作ります。論理式はその解1つ1つがRep-Tileの敷き詰め方と1対1に対応するように作成するので、論理式の解の数を求めることはRep-Tile問題の計数結果を求めることと同じになります。論理式が作れれば、あとは論理式の解の数を求めるプログラムに入力して答えが出るのを待つだけです。

パズルの話から少し脱線しますが、以上のように、ある問題を別の問題に変換することを “帰着” あるいは”還元”と呼びます。計算理論においては問題の難しさの階層分けにおいてよく使われます。直観的には、ある問題Aから別の問題Bに(容易に)帰着可能であるならば、「問題Aは問題Bよりは難しくはない」(問題Bを解く方法があるならば問題Aも計算可能という意味で)と考えることができます。一見異なる問題も本質的な難しさは変わらないということはしばしばあり、問題の「難しさ」って何だろうということを、いろんな種類の問題を横断して深く考え理解する上で役立ちます。
論理式への変換
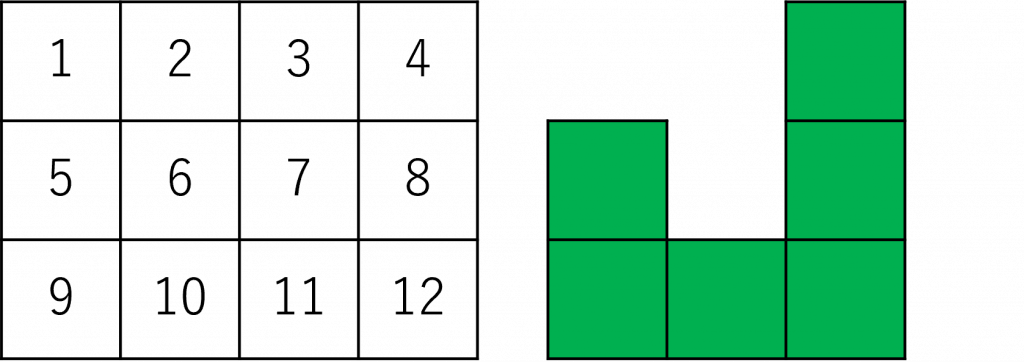
Rep-Tileの敷き詰め問題を論理式へ変換する基本アイデアを説明します。簡単のため、4×3の長方形を敷き詰める領域とし、この領域にJ型のタイルを並べることにします(下図参照)。今、領域の単位正方形に1~12の番号を振っています。全体を敷き詰められるかはいまは考えずに、単に1枚だけJ型タイルを配置することを考えると、(3,5,7,9,10,11)のセルを覆うように置くことができます。ここで、「(3,5,7,9,10,11)のセルを覆うように配置する」ことに対応する変数を1つ用意します。その変数の名前をJ(3,5,7,9,10,11)としましょう。J(3,5,7,9,10,11)は0か1の2通りの値しか取れないとします。J(3,5,7,9,10,11)が1のとき「(3,5,7,9,10,11)のセルを覆うように配置する」こととし、そうでなければそのようには配置しないを意味することにします。このような変数を領域内の配置可能な場所ごとに用意します。
次に、「対象領域を敷き詰める」ことを表す条件について考えてみましょう。敷き詰める対象になっている領域のセルごとに、「そのセルを覆うことができるタイルはちょうど1枚」という条件を表す式を生成します。たとえば、5番のセルの場合、その5番を覆う配置は以下のように6通りあります。全体を敷き詰めることを考えるとありえない配置も含めていますが、ここでは機械的に列挙しています。
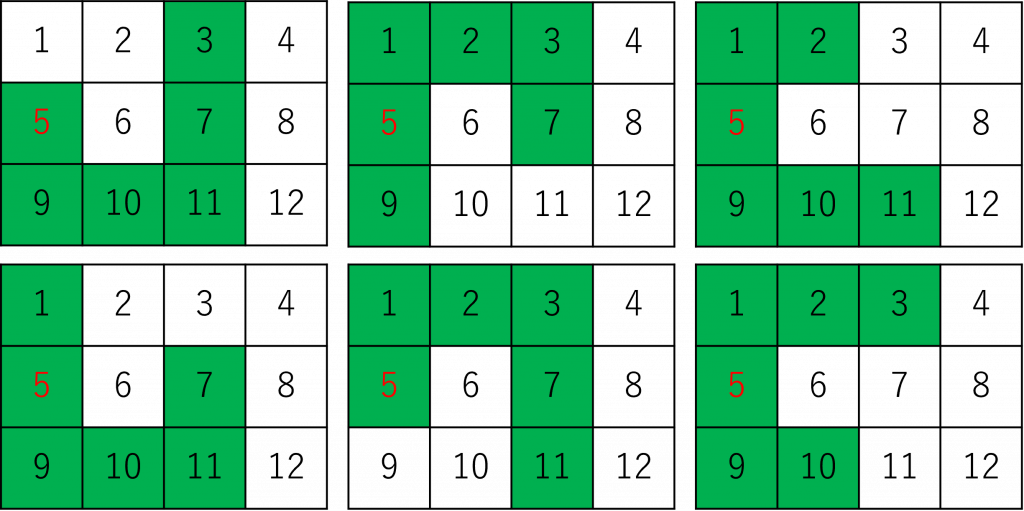
それら6通りの配置に対応する変数の和がちょうど1であるという等式が上で述べたセル5に対する制約になります。すなわち、以下のような式で表せます。
J(3,5,7,9,10,11)+J(1,2,3,5,7,9)+J(1,2,5,9,10,11)
+J(1,5,7,9,10,11)+J(1,2,3,5,7,11)+J(1,2,3,5,9,10) = 1
このような条件式を対象領域のセルごとに生成します。生成したすべての条件を満たすような変数への値割り当て(制約式の解)が求まれば、その割り当てにおいてどの変数が1になっているかを確認すれば敷き詰め方が1つ求まります。
なお、以上の説明では線形等式の形で条件式を表していますが、実際に我々が計算するときにはさらに条件式を命題論理式(真か偽をとる変数と,論理積、論理和、否定の演算からなる式)に変換しています。
論理式の解の計数
命題論理式の解を見つける問題は充足可能性問題(SAT問題)と呼ばれ、NP完全問題と呼ばれる難しい問題と知られています。一方で、これまでにSAT問題を高速に解くための技術が開発されており、SAT問題を解くソルバは検証・知識推論など多くの分野に応用されています。近年、解を1つ見つけるだけでなく、すべての解を求めたりその総数を求めるソルバについても研究されています。我々の研究グループでも命題論理式の解の数を数えるソルバ(モデル計数ソルバ)を開発しています。命題論理式を入力すれば、その式を真にするような変数への真理値割り当てが何通りあるかを答えてくれます。Rep-Tile問題に対して上で述べた方法で生成した論理式の解1つ1つはタイルの敷き詰め方と1対1に対応しますので、計数ソルバでその論理式の解が何通りあるかを数えればRep-Tile問題の敷き詰め方の総数も求めることができます。
最後に、先ほどのJ型の18倍の相似形にJ型タイルを敷き詰める方法の総数を挙げておきます。以下の61桁の数になります。論理式に変換して計数ソルバで解くというアプローチを用いて、さらにタイルの組み合わせの性質も利用する工夫をすることで計数に成功しました。
7709490966015878526472462419226189795822186490162467416571904
おわりに
この記事では、Rep-Tileというパズルを対象にパズルの解を数える方法について紹介しました。今回紹介した、論理式の解の計数問題に還元して解くというアプローチはその他の計数問題に応用できます。つまり、論理式の形に変換できさえすればどのような問題にも利用可能な方法になります。一方で、求解にかかる時間は、どのような論理式を生成するか(符号化と呼ばれる)や論理式の解を数えるソルバの性能に左右されます。そのため、符号化のより良い方法や論理式の解計数ソルバの性能改善が重要であり、この部分が私たちの現在の研究課題となっています。

