経済分析と数理工学
「経済効果」や「経済波及効果」という言葉に聞き覚えがありますか?昨今では,2021年に行われた東京オリンピックや2025年に行われる大阪万博の経済波及効果は◯◯兆円といった形で,聞いた人も多いのではないでしょうか.経済波及効果として示される金額はイメージしやすいかもしれませんが,経済波及効果の意味とはどのようなものなのでしょうか? 本稿では,数理工学の視点から経済波及効果とその計算モデルである産業連関分析について紐解いていきます.
例えば,オリンピックの開催により,建設業の需要が高まったとします.すると,建物を建てるために,鋼,コンクリート,木材,電気,建設機械などが必要となり,鉄鋼業,電力産業など他の産業の需要も高まります.さらに,それらを生産するために,鉄,水,石炭などの原料が求められ,採掘業をはじめとする様々な産業に需要が伝播し,経済全体に広がっていきます.このように,一つの産業の需要が上がることにより,ほかの産業の需要が連鎖的に誘発されます.このような効果のことを経済波及効果と言います. このような効果を算出するには全ての取引をたどって,各産業でどれだけ生産量が上がったかを見れば良いのですが,現実的にはそのような方法で経済波及効果を求めることはほぼ不可能です.そこで,経済波及効果の算出には,産業連関表と呼ばれる経済データを用いた経済分析法である産業連関分析が用いられます.
表 1. 3部門からなる産業連関表
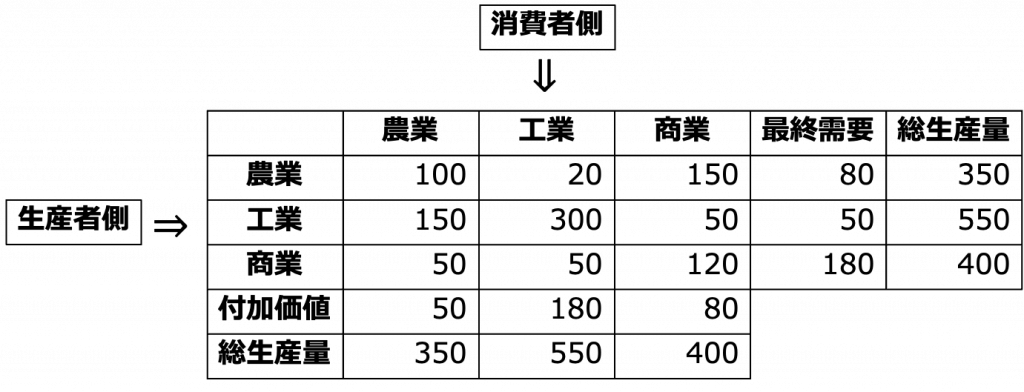
産業連関表は,ある産業からある産業にどれだけ取引を行っているかを表す行列,各産業に対する最終消費者の需要,各産業が生み出す付加価値,各産業の総生産量からなる行列データのことをいいます(表1).表1のように,行列の縦横に各産業が対応づけられ,各要素に取引量が入ります.例えば,(2,1)-要素は工業から農業に150単位の取引があることを示します.このような取引は,農業が製品を生産するために必要な工業の生産量であり,農業の中間投入量を表しています.産業間の取引構造を表す部分を取引表といい,行列\(\mathbf{Z}=\{z_{ij}\}\)で表します.産業数\(n\)をとすると,\(\mathbf{Z}\)は\(n\times n\)-正方行列になります.さらに,各産業に対する最終消費者の需要を最終需要ベクトル\(\mathbf{f}=\{f_{i}\}\),各産業が生み出す付加価値を付加価値ベクトル\(\mathbf{v}=\{v_{j}\}\),各産業の総生産量を生産量ベクトル\(\mathbf{x}=\{x_{i}\}\)で表します.ただし,それぞれのベクトルの大きさは\(n\)です.このように構成される産業連関表の各行は,ある産業が他産業に供給する製品の生産量を表します.すなわち,取引表を横に見ると,生産者として,どの部門にどれだけ生産物を供給したのかがわかります.一方,取引表を縦からみると,製品を作るために他産業からどれだけ生産物を需要したのかを表します.すなわち,需要者(消費者)側の視点から取引表をみていることになります.
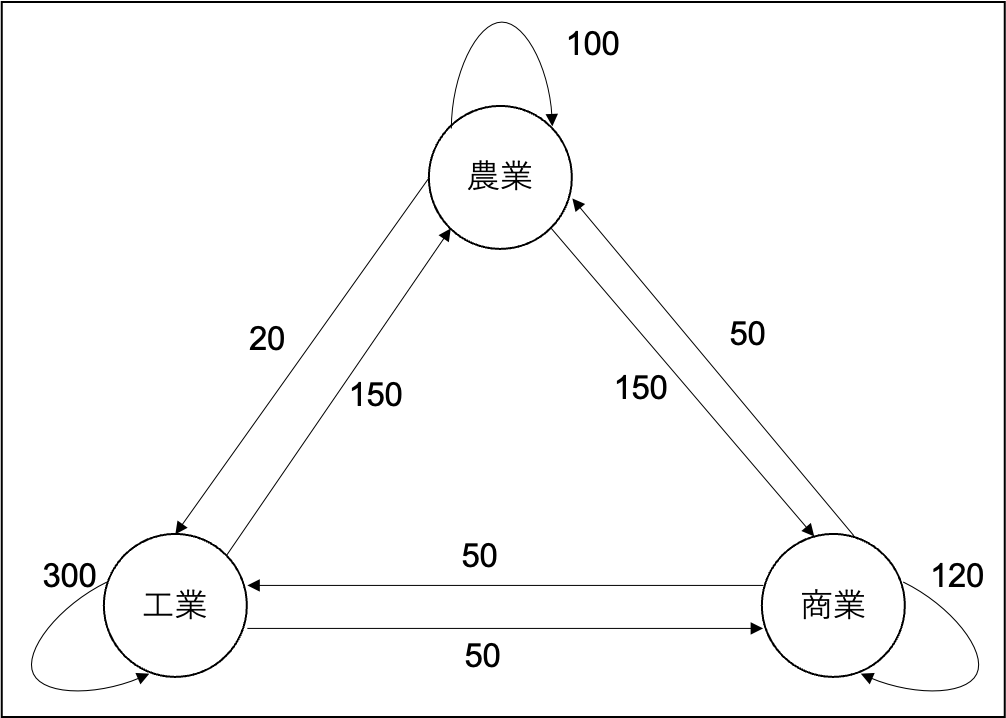
産業連関表は,数理工学でよく用いられるグラフの視点からみるとよりわかりやすくなります.取引表は正方行列なので,重み付き隣接行列と見做すことができます.したがって,取引表\(\mathbf{Z}\)は,点を産業,辺を取引,辺重みを取引量とした重み付き有向グラフとして表すことができます(図1).このとき,取引表を横にみるということは,各頂点(産業)から出ていく重み付き辺をみていることになります.これは,各産業が生産して他の産業に生産物を供給していることを表しています.一方,取引表を縦にみるということは,各頂点(産業)に入ってくる辺をみており,これは他産業から各産業に供給される中間投入物の取引を表しています.
各産業の総生産量は,産業からほかの産業に供給する取引量(すなわち生産量)と最終需要に対する生産量の和であるので,\(x_i=\sum_{j=1}^n z_{ij}+f_i\)が成り立ちます.これは,産業連関表の各行和が各産業の総生産量に等しいことを表します.これを行列形式で書くと,\(\mathbf{x} = \mathbf{Z1} + \mathbf{f}\)となります.ただし,1は各要素が1である\((n\times 1)\)ベクトルです.一方,各列和をとると,\(x_j=\sum_{i=1}^n z_{ij}+v_j\)も成り立ちます.このように,産業連関表は各行和と各列和が等しいという性質を持っています.
ここで,\(\mathbf{Z}\)の各要素\(z_{ij}\)に対して,\(a_{ij}=z_{ij}/x_j\)とします.すると,\(a_{ij}\)は,産業の生産量1単位を産出するのに必要な産業からの中間投入額を表し,投入係数と呼ばれます.そして,投入係数を要素とする行列を\(\mathbf{A}=\{a_{ij}\}\)投入係数行列と呼びます.このとき,
\[\mathbf{x} = \mathbf{Z1} + \mathbf{f} \]
\[\mathbf{x} = \mathbf{Ax} + \mathbf{f} \]
\[(\mathbf{I}-\mathbf{A})\mathbf{x} =\mathbf{f} \]
が得られます.ここで,\(\mathbf{I}-\mathbf{A} \)は逆行列を持ち,\(\mathbf{x} = (\mathbf{I}-\mathbf{A})^{-1}\mathbf{f} \)が得られます [1].逆行列\(\mathbf{L}=(\mathbf{I}-\mathbf{A})^{-1}\)は,レオンチェフ逆行列と呼ばれ,産業連関分析の根幹であると言っても過言ではないほど重要な行列です.レオンチェフ逆行列は,最終需要が1単位増えたときに,直接間接的に誘発される生産量,つまり経済波及効果を表しています.レオンチェフ逆行列は,\(\mathbf{L}=\mathbf{I}+\mathbf{A}+\mathbf{A}^2+\cdots\)と行列の無限級数として展開することができます [1,2].最終需要ベクトルをかけると\(\mathbf{L}\mathbf{f}=\mathbf{f}+\mathbf{A}\mathbf{f}+\mathbf{A}^2\mathbf{f}+\cdots\)となり,右辺の第一項は最終需要に対する直接的な生産を表します.第二項は,最終需要によって誘発された間接的な生産を表します(第一次波及).第三項は,第一次波及によって誘発された間接的な生産(第二次波及)というように無限に波及が続いていくことを表します.経済波及効果は,このような最終需要によって誘発された直接間接的な生産量の和によって定義され,算出されています.また,経済波及効果はある意味ネットワークを無限に重ね合わせたものとして見做すことができます.行列\(\mathbf{A}\)を重み付き隣接行列とみなすと,\(\mathbf{A}^n\)の\((i,j)\)-成分は\(i\)から\(j\)への相違なる長さの重み付き路となります.これはまさに\(n\)次波及に対応します.また,\(a_{ij}<1\)なので,波及が繰り返されるにつれて,波及効果が徐々に弱まっていくことも表現しています.
表1を例にレオンチェフ逆行列を計算してみます.まず,投入係数行列は以下のようになります.
\[{\bf A} = \left[ \begin{array}{rrr} 100/350 & 20/550 & 150/400 \\ 150/350 & 300/550 & 50/400 \\ 50/350 & 50/550 & 120/400 \end{array} \right] =\left[ \begin{array}{rrr} 0.286 & 0.036 & 0.375 \\0.429& 0.545& 0.125 \\ 0.143 & 0.091& 0.300 \end{array} \right] \]
よって,レオンチェフ逆行列は以下のように求まります.
\[{\bf L} = \left(\left[ \begin{array}{rrr} 1& 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0& 1 \end{array} \right]-\left[ \begin{array}{rrr} 0.286 & 0.036 & 0.375 \\0.429& 0.545& 0.125 \\ 0.143 & 0.091& 0.300 \end{array} \right]\right)^{-1} =\left[ \begin{array}{rrr} 1.819 &0.353 &1.038\\ 1.885 &2.647&1.482\\ 0.616&0.416&1.832 \end{array} \right] \]
今,農業の最終需要が10単位増えるとしましょう.最終需要の変化を表すベクトルをとすると,誘発される各産業の生産量は,
\[ {\bf L}\Delta{\bf f}=\left[ \begin{array}{rrr} 1.819 &0.353 &1.038\\ 1.885 &2.647&1.482\\ 0.616&0.416&1.832 \end{array} \right] \left[ \begin{array}{r} 10\\ 0\\ 0 \end{array} \right] = \left[ \begin{array}{r} 18.19\\ 18.85\\ 6.16 \end{array} \right]\]
となります.すなわち,農業の最終需要が10単位増えると,直接間接的に農業の生産が18.19, 工業の生産が18.85, 商業の生産が6.16ほど生み出されることがわかります.これが,農業の最終需要が10単位増えたときの経済波及効果となります.ポイントとしては,直接的に増加した生産は最終需要による1単位にも関わらず,経済全体を通して,さまざまな生産が引き起こされ,結果的に大きなインパクトになるということです.そして,最終需要がどれだけ上がるのかさえ推計できれば,レオンチェフ逆行列を用いることによって経済波及効果を求めることができます.このように産業連関表を用いた経済分析を産業連関分析と呼びます.産業連関分析は,経済波及効果をはじめとする様々な経済分析に用いられています.実際,東京オリンピックの経済波及効果も東京都の産業連関表を用いて推計されています[3].例えば,東京オリンピックの経済波及効果は,東京都でおよそ20兆円,全国でおよそ32兆円と試算されています [3].これらの金額だけを見ると,オリンピックだけでそんなに生産が生まれるのか不思議に思うかもしれませんが,オリンピックのチケット代だけでなく,あらゆる産業の生産が生じるのでこのように大きな金額になるのです.
これまで見てきたように,産業連関表はある種のネットワークとして表すことができます.産業連関表はその経済システムの構造を表していると見做すことができます.産業構造がどうなっているのかを解析する手段として,そのネットワーク構造に注目して分析するといった取り組みが古くから行われています.
産業連関分析を提案したレオンチェフは,産業連関表から経済構造を分析するために三角化と呼ばれる手法を提案しました [4].三角化とは,行列の各行各列を並び替えることによって上三角成分を最大化させる並び順を求めることを指します.
産業連関表に三角化を適用すると,複雑に絡み合った産業取引構造から主要なサプライチェーン構造を抽出することができます.サプライチェーンは,原料から製造過程を通じて最終消費者に向かうまでの一連のプロセスのことをいいます.三角化を用いて,このようなサプライチェーン構造を抽出することにより,産業の性質や経済構造の変化の分析に役立てています [5].
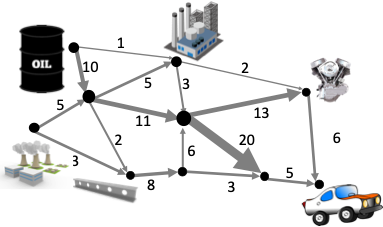
産業連関分析分野で知られている三角化は,数理工学分野においては最小重みフィードバック辺集合問題と呼ばれ,Galey and Jonsonの本にも載っており,典型的な組合せ最適化問題として知られています[6].最小重みフィードバック辺集合問題は,重み付き有向グラフGが与えられて,GからSに属する辺を削除したグラフが有向無閉路グラフ(DAG)になるような最小の辺部分集合を見つける問題です.産業連関表に照らし合わせてみると,DAGのソースに近い頂点(産業)がサプライチェーンの上流,シンクに近い頂点が下流に対応します.残った部分は最大のDAGとなっているので,主要なサプライチェーンを抜き出したことに対応します.図2の例では,最終製品が自動車となるサプライチェーンがDAGとして表現されています.
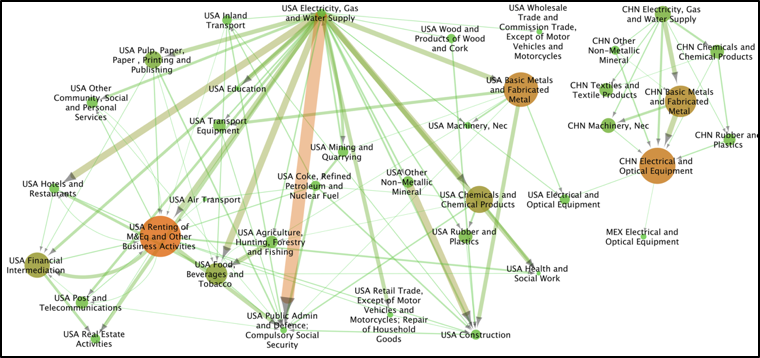
産業連関分析は,経済活動に伴うCO2などの環境汚染物質を効率的に抑制したり,排出責任の所在を明らかするために取引を通じた排出物質の流れを分析することにも利用されています.その一つとして,産業間協力による効率的な排出削減を行うために,産業連関表を重み付きグラフとして表し,グラフクラスタリングを適用することによって産業間の関係を分析する試みも行われています [7,8].また,取引ネットワーク上の波及経路に注目し,サプライチェーン全体を見たときにどのようなパスや取引,産業が環境負荷を与えているのか,もしくはどのような国が“間接的”に取引相手として重要なのか等を産業連関理論を用いて解析するといった研究も行われています [9].図3は,ネットワーク理論と産業連関分析を用いて,米国の最終需要によって発生したCO2 に対する高環境負荷ネットワークを抽出・可視化したものになります.このように産業構造をネットワークとしてみることにより,様々な見通しが良くなったりすることも多くあります.
本稿では,産業連関分析と数理工学のつながりを中心に紹介しました.経済波及効果がどのようにして算出されているのか,また数理工学とどのようにつながっているのかについて.産業連関表はオープンソースとして簡単に手に入れることもできます.例えば,政府が作成した日本産業連関表はe-Stat (https://www.e-stat.go.jp) に公開されています [10].実際に計算してみるのも面白いかもしれません.
参考文献
[1] Miller, R.E., Blair, P.D. (2009) Input-output analysis: Foundations and Extensions, Cambridge University Press.
[2] Waugh, F.V. (1950) Inversion of the Leontief matrix by power series. Econometrica, 18, 142–154.
[3] 東京都 オリンピック・パラリンピック準備局,東京2020大会開催に伴う経済波及効果 (試算結果のまとめ)https://www.2020games.metro.tokyo.jp/9e1525ac4c454d171c82338c5a9b4c8a_1.pdf
[4] Leontief, W. (1963) The structure of development. Scientific American, 209(3):148–167.
[5] Kondo. Y., (2014) Triangulation of input-output tables based on mixed integer programs for inter-temporal and inter-regional comparison of production structures. Journal of Economic Structures, 3(1):2.
[6] Garey, M.R., Johnson, D. S. (1979) Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman & Co., New York, NY, USA.
[7] Kagawa, S., Suh, S., Hubacek, K., Wiedmann, T., Nansai, K., Minx, J. (2015) CO2 emission clusters within global supply chain networks: Implications for climate change mitigation. Global Environmental Change, 35:486–496.
[8] Kanemoto, K., Hanaka, T., Kagawa, S., Nansai, K. (2018) Industrial clusters with substantial carbon-reduction potential, Economic Systems Research, 31(2), pp. 248–266.
[9] Hanaka, T., Kagawa, S., Ono, H., Kanemoto, K. (2017) Finding Environmentally Critical Transmission Sectors, Transactions and Paths in Global Supply Chain Networks”, Energy Economics, Volume 68, Elsevier, 2017, 44–52.
[10] 政府統計の総合窓口(e-Stat)https://www.e-stat.go.jp/

