ミニ特集「セキュリティ」:暗号・トリック・マジック
セキュリティと聞くと,暗号を使って秘密の情報を保護したり,不正者によるアクセスを遮断したりするようなイメージを抱く方が多いと思います.そのようなイメージは間違いではありませんが,セキュリティ技術の限られた一面を示すものでしかありません.この記事では,多彩で多様なセキュリティ研究の一端を紹介したいと思います.
セキュリティ研究の歴史
暗号技術の起源は古く,紀元前には原始的な暗号が使われていたとも言われています.しかし,暗号やセキュリティが学術的な意味での研究対象となったのは,比較的最近のことです.情報通信が未発達な時代においては,暗号を必要とする人や組織はきわめて限られており,また,暗号技術自体も単純で即物的なものに終始していました.エニグマ暗号の解読に注力したアラン・チューリングや,情報理論的な観点から暗号の安全性を論じたクロード・シャノンといった(非常に大きな)例外はありますが,歴史的に見ると,暗号は,それほど多くの研究者の興味を惹くものではありませんでした.
一方,1970年代に入ってコンピュータが身近なものとなり,複雑で大規模な計算が効率よく実行できるようになってくると,従来では考えられなかったアプローチから暗号を作ろうとする試みが出てきます.とくに,「数学的な難問」を巧みに利用した公開鍵暗号の深遠さは多くの研究者を魅了し,暗号・セキュリティ研究のコミュニティが徐々に形成されてゆきます. 当時は,驚異的な速度で発達する情報通信技術が,我々の生活を大きく変えると期待されていた時代でもあります.リアルの世界の様々な行為を電子的に実現するための研究が盛んに行われましたが,その多くは,比較的早い段階で大きな壁に直面してしまいます.たとえば,メールやSMSを使って「じゃんけん」をするケースを考えてみましょう.じゃんけんではプレーヤー全員が同時に手を出す必要がありますが,リアルの世界のじゃんけんでは「同時性」を厳密に追求することはありません.たとえコンマ何秒という時間差で「後出し」があったとしても,生身の人間であれば,その僅かな時間差にはほとんど意味がないという暗黙の了解があるためです.一方,メールを使ってじゃんけんをする場合,コンマ何秒という時間差があれば圧倒的に有利になるため,同時性を厳密に追求する必要が出てきます.とはいえ,通信の遅延時間まで考えて同時性を実現することは,まったく現実的ではありません.「後出し」が発生することは避けられないという前提の下,不正行為を防ぐための技術として,セキュリティ研究に出番が回ってきます.
ビットコミットメント
じゃんけんの同時性を実現する安直な仕組みとしては,信頼できる審判を一人決め,その審判にプレーヤーの出す手を預かってもらう方法が考えられます.すなわち,プレーヤーは自分の出す手を暗号化通信で審判に伝え,審判は,全員の手が出揃った後にはじめて結果を公表する,というものです.信頼できる管理者に重要な情報を託すことは,21世紀の今日の商用サービス等でも多く行われていますが,セキュリティ的には上策とは言えません.管理者が不正を行う可能性もありますし,外部からの攻撃により管理者の持つ秘密情報が漏洩するリスクも存在します.また,管理者が公正に操作を行ったとしても,そのことを第三者に立証することは「悪魔の証明」となり非常に困難です.勝負に負けたプレーヤーから不正の可能性を訴えられたとしても,審判(管理者)は,自身の無実を示すことができません.
信頼できる管理者を置かずにじゃんけんを実現する方式としては,ビットコミットメントと呼ばれる技術を利用することが考えられます.ここで利用されるのが暗号学的ハッシュ関数(ハッシュ関数)と呼ばれるものです.ハッシュ関数とは,(性質1:一方向性) 与えられた x に対して y=f(x) を計算することは簡単だが,与えられた y に対して y=f(x) となる x を探しだすことは難しい,(性質2:衝突困難性) f(x_1)=f(x_2) となる2つの異なる値 x_1, x_2 を探しだすことは難しい,といった性質を持つ関数です.じゃんけんのグー(チョキ,パー)を出したいプレーヤーは,G(C, P)から始まるランダムな文字列を x として選び,f(x) の値を自分の手の「ビットコミットメント」として宣言します.下図は,SHA-1と呼ばれるハッシュ関数でグー,グー,パーのビットコミットメントを計算した例です.
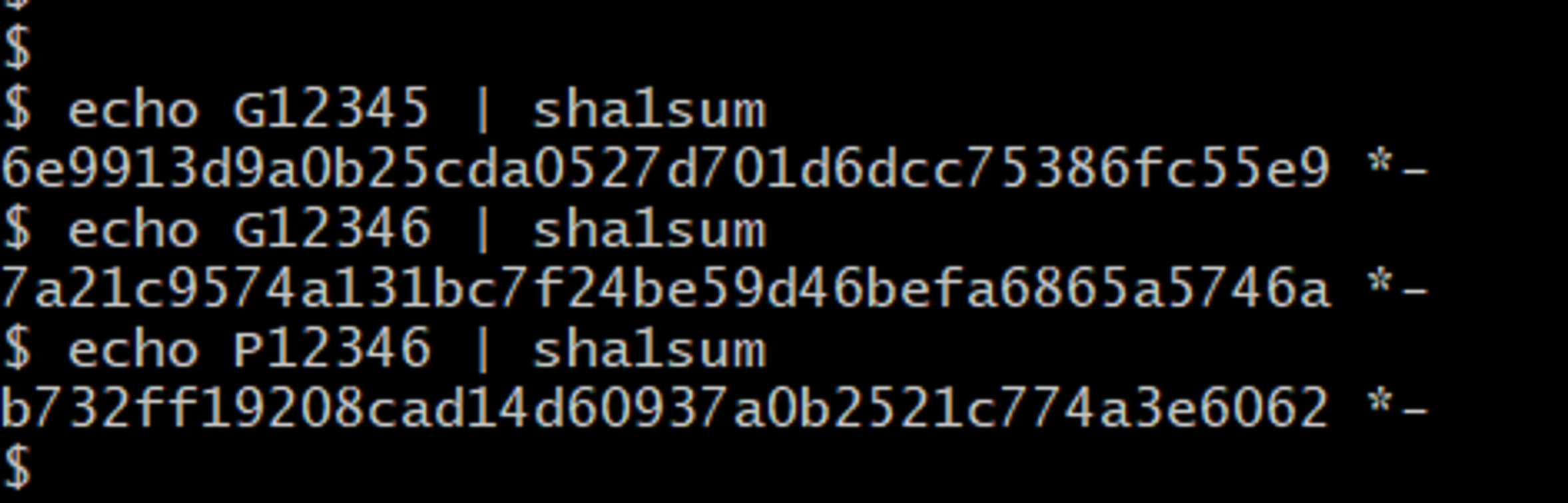
全プレーヤーがビットコミットメントを宣言した後に各プレーヤーが x に相当する文字列を公表することで,それぞれの手の勝敗を決めます.他のプレーヤーのビットコミットメントを見ても,そこに隠されている手が何かはわからないため,ビットコミットメントの宣言は同時である必要はありません.また,他のプレーヤーが x の値を公表した後に自分の手を変更しようとしても,既に宣言したビットコミットメントの値を変えることはできませんので,いわゆる「後出し」はできないことになります.将棋でいうところの「封じ手」を数学的に実現したもの,と考えるとわかりやすいかもしれません.ビットコミットメントは非常に単純な仕組みですが,情報通信の同時性の問題を回避し,プレーヤーの不正を防止するのに有効に機能します.
紛失通信(oblivious transfer)
じゃんけんからは少し離れ,別の例を考えてみましょう.あるニュースサイトでは,複数のニュース記事を有料で販売しています.記事のタイトルは誰でも見ることができますが,本文を読むためには費用を支払って記事データを入手する必要があります.あなたは,販売されている記事のうち1本を読みたいと考えていますが,どの記事に興味を持っているかはサイト側に知られたくありません.自分の選択を伏せたまま,必要な記事データだけを入手することは可能でしょうか?
一見すると,そんなムシの良い方法なんてあるわけないと思ってしまいますが,公開鍵暗号を使えば,この問題を解決することが可能です.公開鍵暗号とは,「暗号化に使う鍵」と「復号に使う鍵」が異なるタイプの暗号で,鍵の生成時に使われた特定の秘密情報を知らない限り,暗号化鍵から復号鍵を計算することはできません. この公開鍵暗号と,昔からある共通鍵暗号(暗号化と復号に同じ鍵を使う暗号)を組み合わせ,次のようなやりとりで記事データの配布を行うことを考えてみましょう.ここでは簡単のため,ニュースサイトの経営者をアリス,記事の購入者をボブとし,ニュース記事が全部で5本あるとして説明を行うことにします.また,鍵 k を用いて平文 m を暗号化する操作を E(k,m),鍵 k を用いて暗号文 c を復号する操作を D(k,c) と書くことにします.
- アリスは,記事ごとに異なる公開鍵暗号の鍵組を生成する.以下では,記事 i の暗号化鍵を e_i , 復号鍵を d_iと表記する.
- アリスは,それぞれの記事の暗号化鍵 e_1, …, e_5 をボブに伝達する.
- ボブは,共通鍵暗号の鍵 k をランダムに生成し,所望の記事の暗号化鍵 e_i で k を暗号化して得られる暗号文 c=E(e_i, k) をアリスに送信する.ただし,どの暗号化鍵 e_i を使ったかはアリスに知らせない.
- アリスは,j=1, 2, …,5 のそれぞれに対し,k_j=D(d_j,c) として5個の鍵データ k_1,…,k_5 を計算する. ボブの選んだ i の値に対し k_i = k となっている点に注意.
- アリスは,j=1, 2, …,5 のそれぞれに対し,鍵 k_j を使って j 番目の記事データ a_j を暗号化し,c_j=E(k_j, a_j) をボブに送信する.
- ボブは,自分の選んだ鍵 k を使ってc_i を復号し,D(k,c_i)=D(k_i, E(k_i, a_i))=a_i を計算することで所望の記事を入手する.
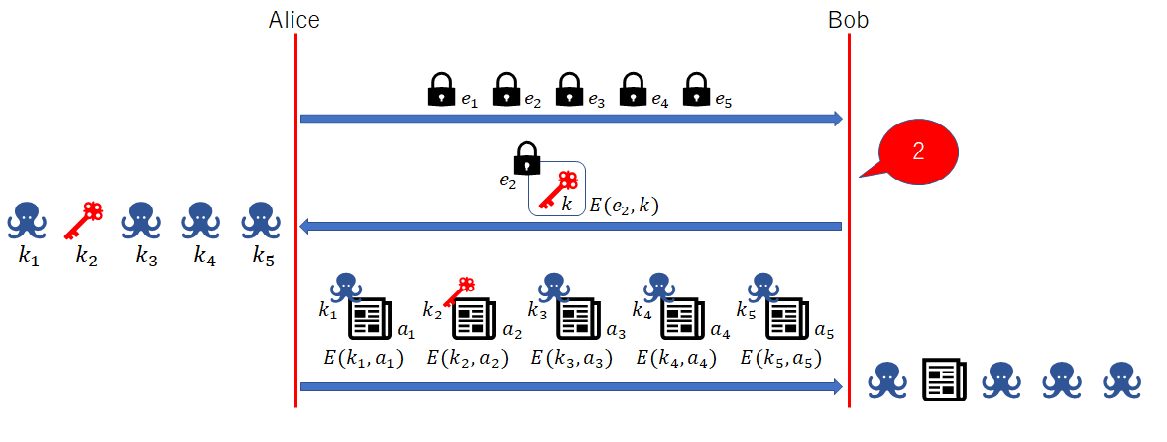
アリスは,ステップ4で5個の鍵データを計算することになります.この5個の鍵のうち,どれか1つはボブが選んだ k になっているはずですが,それがどれなのかはアリスにはわかりません.したがって,アリスはボブがどの記事を選択したのかを知ることができません.ステップ5では,5本の記事をそれぞれ暗号化してボブに送信しています.アリスとしては,ボブが1本の記事の料金で全部の記事を読んでしまうのではないかというところが心配になるところですが,その点も抜かりはありません.ボブは,アリスが計算した5個の鍵のうち自分が選んだ鍵 k 以外のものが何なのかを知ることができないので,たとえ手元に 5本の記事が暗号化されて届けられたとしても,その中で復号に成功するのは,自分が最初に選んだ1本の記事だけとなります.
ここで紹介したのは,oblivious transfer(日本語では紛失通信や忘却通信と訳されます)と呼ばれるテクニックです.公開鍵暗号と共通鍵暗号を組み合わせることで絶妙なトリックを作り出し,個人情報を守りつつ,不正な情報入手も防ぐ仕組みが構成されています.
マルチパーティ計算
それほど頻繁ではありませんが,複数の人が所有する「オープンにできない情報」に基づいて,なんらかの値を計算したいといったシチュエーションがあります.たとえば,同じテストを受けた2人の学生であるアリスとボブが,それぞれ自分の点数は伏せたままで,どちらが良い点数を取ったのか判断したいといったケースを考えてみましょう.テストは100点満点で,アリスの点数を a, ボブの点数を b とします.アリスもボブも,自分の点数は相手に伝えたくありませんが,嘘をついたり不正を行ったりする動機はなく,両名とも以下の手順を正しく正直に実行するものとします.
- ボブは公開鍵暗号の鍵組 (e, d) を準備し,暗号化鍵 e をアリスに知らせる.
- アリスは大きな整数 r をランダムに選び,z = E(e, r) – a を計算してボブに伝える.
- ボブは以下の式に従って v_0, …, v_100 を計算し,そのすべてをアリスに送る.ただし,f は暗号学的ハッシュ関数である.
- v_i = f(D(d, z + i)) (0 ≦ i ≦ b)
- v_i = f(ランダムな値) (b < i ≦ 100)
- アリスは v_a = f(x) かどうかを調べ,a ≦ b かどうかを判定してボブに結果を伝える.
- v_a = f(r) ならば a ≦ b
- v_a ≠ f(r) ならば a > b
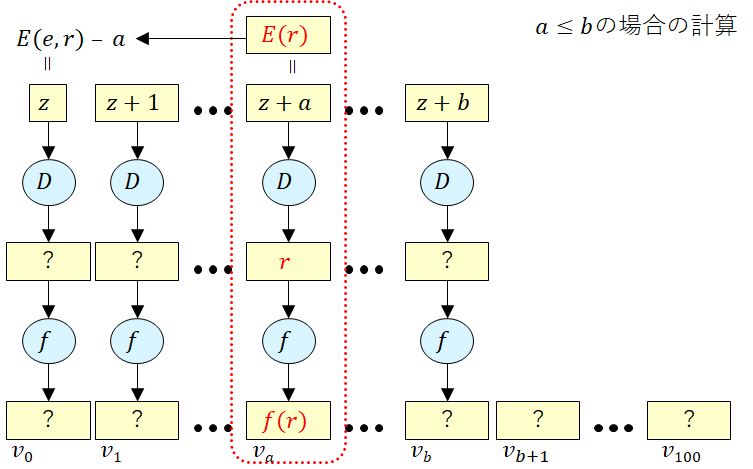
ステップ3の計算について,もし a ≦ b なら v_a の計算には最初の式が使われ,v_a = f(D(d, z+a)) = f(D(d, E(e, r))) = f(r)となります.一方,a > b なら v_a の計算には2番目の式が使われ,v_a = f(ランダムな値) ≠ f(r) となります. このことから,上記の計算で a, b の大小関係が正しく計算できることがわかります.ボブはステップ 3で101個の値 v_0, …, v_100を計算しますが,たとえ a ≦ b であったとしても,どの z+i が E(e, r) と一致するかを判別することができませんので,アリスの点数 a を知ることができません.アリスについても,i≠a となる i に対して D(d, z+i) が何になるか推測できないため,v_i (i≠a) が最初の計算式で得られたものなのか,2番目の計算式で得られたものなのかを判別することができず,ボブの点数 b を特定することができません.結果として,お互いの点数は伏せたままで,どちらが高得点を取ったのかという結果だけを正しく計算できたことになります.
ここで示したのは,複数のユーザー(パーティ)がプライベートで持っている情報に基づき,情報を秘匿したまま計算を実行する「マルチパーティ計算」の一種です.通常のコンピュータで計算できる任意の関数は,たとえそれがどれほど複雑なものであったとしても,マルチパーティ計算で計算できることが知られています.魔法を使ったかのように不思議な計算ができる,という意味で「マジックプロトコル」と呼ばれることもあり,大きな活用可能性を秘めた技術だと考えられています.
おわりに
この記事で紹介したような内容は,1980年代から1990年代にかけて盛んに研究されていました.非常に多くの研究成果が生み出されましたが,当時はまだ社会の情報化が十分には進んでおらず,せっかくの研究成果の多くが,実用化に結びつくことなく放置されてしまっています.それから30年が経過し,現在の私達は,当時の人々が想像していた情報化社会の中を生きています.肌身離さずスマートフォンを持ち歩き,いつでも,どこでも,強力な計算パワーと高速な情報通信ができる環境の中に身を置いています.その一方,個人情報の過度な集約が社会的な問題となり,自分の情報は自分で守らざるを得ない,あまり嬉しくない状況も生まれつつあります.このような時代だからこそ, 現代人の視点から30年前の研究成果を眺めることで,何か見えてくるものがあるのではないでしょうか.

