特集「新型コロナと情報」:数理生物学・複雑系科学の視点から
COVID-19パンデミックについては現在も状況が刻一刻と変化しており、個人的にはまだまだ予断を許さないものと思われます。私は感染症疫学の専門家というわけではありませんが、「8割おじさん」として有名な厚労省クラスター対策班の西浦博先生は以前から数理生物学学会で顔を合わせる研究仲間でもありますので、数理生物学・複雑系科学の観点から、個人的に注目している情報をかいつまんでシェアしたいと思います。
実効再生産数
今回の件で最も印象的なことのひとつは、実効再生産数という言葉がテレビのワイドショーでも取り上げられるなど、感染症流行の数理モデル研究にスポットライトが当たったことです。感染症数理は、多様な数理生物学の研究分野の中でも最も長い歴史をもち、それは1927年のケルマックとマッケンドリック[1]のいわゆるSIRモデル
\begin{align}
&\frac{d S(t)}{dt}=-\beta S(t) I(t)\nonumber\\
&\frac{d I(t)}{dt}=\beta S(t)I(t)-\gamma I(t) \tag{1}\\
&\frac{d R(t)}{dt}=\gamma I(t)\nonumber
\end{align}
に遡ります。\(S(t), I(t), R(t)\)はそれぞれ時刻\(t\)における感受性人口(susceptibles: 感染する可能性のある人口)、感染人口(infectives: 感染していてかつ感染させる能力のある人口)、隔離された人口(recovered/removed: 回復して免疫をもつ者もしくは隔離者・死亡者)を表します。 (1)式中の\(S(t)\)を感染初期の値\(S(0)\)に置き換えた線形化方程式を考えることにより、感染者人口\(I(t)\)が指数関数的に増大する条件
$$R_0=\frac{\beta S(0)}{\gamma}>1\tag{2}$$
が求まります。この\(R_0\)が、いわゆる基本再生産数と呼ばれるものです。しかし、もともとSIRモデルは局地的な封鎖人口における伝染病の急速かつ短期的な流行ダイナミクスをモデル化するものであるため、今回のCOVID-19のようなパンデミックにおける基本再生産数の推定は容易ではありません。一般に、流行が地域、国をまたいで広がっていく場合には病原体の感染能力の変動や、潜伏期間、ロックダウンなどの人間の行動変容により、その値は時々刻々と変化していきます。
そこで、SIRモデル以降、潜伏期間中の感染者数\(E(t)\)を加えたSEIRモデルや、さらに他者を感染させる能力をもつまでの「時間遅れの効果」を組み込んだモデルなど、さまざまな現実的な状況に対応するモデルへの拡張が行われてきており[2]、それらの最新の研究結果にもとづいて、感染者数や感染日、発症日などの調査データからその日その日の実効再生産数(ある時刻において感染者ひとりが単位時間に感染させる他者の数の期待値)を推定するということが行われ(西浦先生はこの分野における世界的権威です)、自治体や政府の緊急事態宣言などの行政の対応につなげられています。
(2)式の基本再生産数の算出は、感染者が未感染者に病気を移す確率が全員同じという仮定にもとづきますが、近年の複雑ネットワーク[3]における感染症数理の研究は、スーパースプレッダーと呼ばれるたくさんの人に病気を移す人の存在が実効再生産数を増大させ感染爆発を引き起こすことを示しており、初期のHIV感染症流行やコンピューターウィルス拡散などの主要因とも考えられています。COVID-19における日本のクラスター対策も、そのような複雑系科学研究の知見にもとづくものともいえます。
日本の実効再生産数の変動については、最近は東洋経済新聞社の特設サイト[4]でも見られるようになっていますが、5月の末から6月にかけて再び1を超えた週もあり、まだまだ流行が収束したとはいえない状況にあることがわかります。世界的にも一刻も早い経済活動や学校の再開が望まれているところですが、今後とも科学にもとづく行政の対応や政府の経済対策が実行されることを願っています。
歴史は繰り返す
実行再生産数の推定などの、現在の流行状況の分析が大事であることはいうまでもないことですが、新型感染症のパンデミックは歴史的に繰り返されてきたものであり、過去のパンデミックや社会の状況を紐解くこともCOVID-19対策に資するものと思われます。そこで、1993年にアメリカの「日本学」に関する学会の学会誌に掲載された、日本におけるスペインかぜ流行と行政の対応についての調査研究[5]について簡単にご紹介したいと思います。
いきなりですが、9ページの「地図1」(県ごとの死亡率分布)が衝撃的です。島根、鳥取などCOVID-19では感染者が少ない県の死亡率が高いです(6.0-7.9/千人、COVID-19の千倍以上)。日本のスペインかぜによる死亡率は、今回のCOVID-19と同じように、世界的には最低レベルだったのですが、その理由として「1918年4月から6月にかけて世界的に流行した『軽度』のインフルエンザへの感染による獲得免疫と、その年の後半に流行した『重度』のインフルエンザに対する地域社会の対応の質」があげられており、さらに、大都市よりも地方での死亡率が高かった理由については、「宮崎県、埼玉県、鏡山市、愛媛県、島根県、徳島県の罹患率が非常に高かったことは、これらの県が『軽度』の波をほとんど逃れたため、10月から11月にかけてのより活発なウイルスに対する免疫力が低かったことを示唆している」と書かれています。この仮説やシナリオがCOVID-19にも当てはまるとすると、現在感染者数の少ない岩手、鳥取、島根などは、今後危惧される第2波に対してより一層警戒する必要があると思われます。
他にも「(当時の)厚生省の報告書の中に1890年のインフル流行についての記述がある」とか「東京では、警視庁公衆衛生課の課長は、韓国では当局が礼拝や娯楽のために人が集まることを厳しく禁じていると指摘したが、『日本ではできない』と付け加えた。その理由を知ることは興味深い」といった記述もあります。さらに「公式報告書では、1918年の『スペイン・インフルエンザ』大流行時にも各国で熱く議論された、飛沫感染による感染症の伝播を防ぐためのマスクの有効性について論じている」とも書かれています。「自粛問題」も「マスク論争」も100年前に起こっていたようです。
パンデミックの法則
今回のCOVID-19パンデミックについて、複雑系科学研究者として最も気になる点は、各国ごとの流行状況の多様性です。特に、本庶佑京都大名誉教授も「法的に比較的緩やかなシステムで、死者と感染者がこんなに少ないのは、多くの医学者にとっても謎」とコメントされていましたが、日本の死亡率(死亡者数/人口)の低さについては、さまざまな仮説が取り沙汰されているものの、まだ決定版といえる研究はないといった状況かと思われます。
図の緑と青のカーブは、各国の感染者数、死亡者数などがまとめられたサイト[6]からデータをダウンロードして、今年4月と6月の時点での各国の死亡率(人口100万人あたりの累計死亡者数)を高い順に並べてみたものです。欧州のOECD原加盟国が上位に集中している一方、発生国の中国に近いアジア諸国の死亡率が低いのが印象的です。
横軸の順位(Rank)は死亡率の累積分布に相当し、青や緑のカーブの逆関数の微分が死亡率の分布に対応するため、世界各国の死亡率の分布が対数正規分布に近いものにみえるのも興味深いです。これは今回のCOVID-19パンデミックが従う法則ともいえるものではないかと思っています(各国の死亡率が、いわゆる乗算過程に従ってランダムウォークしているように見えます)。この分布が、国ごとのどのようなパラメータの多様性に起因するものなのか、調べてみようと考えているところです。
なお、図の赤線は、6月の死亡率の順位に合わせた各国の致死率(死亡者数/感染者数)のグラフですが、致死率は各国ごとの感染者のサンプリングエフォートやバイアス、医療の状況にも依存するせいか、死亡率にみられる多様性のパターンは見えていないように思われます。
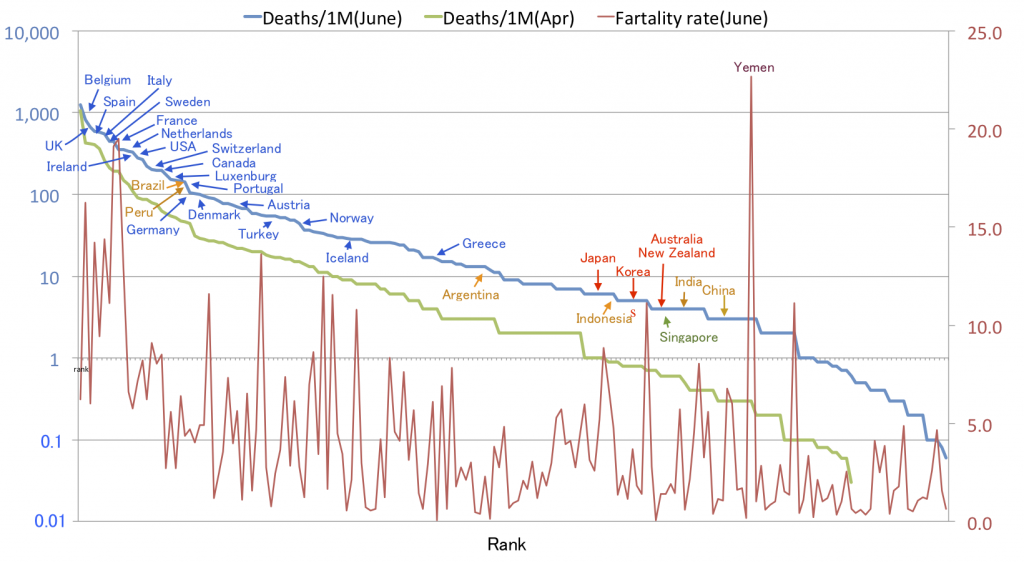
世界各国のCOVID-19死亡率順位(人口100万人当たり累計死亡者数)(青:6月4日、緑:4月17日)、致死率(赤、死亡者数/感染者数)、青字:OECD原加盟国、赤字:OECDアジア加盟国、橙字:OECD加盟申請中、緑字:その他
2020年度日本数理生物学会大会のお知らせ
最後に告知をさせてください。今年度の日本数理生物学会大会は9月20日~21日の3日間オンラインで開催されます[7]。数理生物学会では、感染症数理を含む、さまざまな生物学上の問題についての理論研究が多数発表されます。今回は、学生は非会員も聴講無料となっていますので、この分野に興味のある学生さんはぜひ登録して聴講してみてください。さらに今回は本学会初の試みとして、高校生を対象とするセッション(第一線の研究者によるレクチャー「数理生物学への招待」、懇親会、進学相談会)も予定しています。「生物が好き、数学も好き、コンピュータも好き」という高校生の皆さんは奮ってご参加ください。
1. W. O. Kermack and A. G. McKendrick (1927) Contributions to the mathematical theory of epidemics I、 Proceedings of the Royal Society 115A:700-721. (reprinted in Bulletin of Mathematical Biology 53(1/2):33-55, 1991).
2. 稲葉寿(編著)、感染症の数理モデル、培風館、2008
3. 増田直紀、今野紀雄、複雑ネットワーク:基礎から応用まで、近代科学社、2016年
4. 東洋経済ONLINE 新型コロナウィルス 国内感染の状況, https://toyokeizai.net/sp/visual/tko/covid19/ (参照2020年6月1日)
5. G. W. Rice and E. Palmer, Pandemic influenza in Japan, 1918-19: Mortality patterns and official responses, The Journal of Japanese Studies, 19: 389-420, 1993.
6. Worldmeter, COVID-19 CORONAVIRUS PANDEMIC, https://www.worldometers.info/coronavirus/ (参照2020年6月1日)
7. 2020日本数理生物学会年会, https://sites.google.com/view/jsmb2020conference (参照2020年6月1日)
時田 恵一郎
名古屋大学 大学院情報学研究科 複雑系科学専攻 教授
専門は統計力学、数理生物学、多様性の科学

