実験できない現象をコンピュータの中で実現する:形状最適化と逆問題
はじめに
実際に見たり感じたりすることのできる現象であれば,実験で再現することができるかもしれません.もしも,その現象を支配する数理モデル(ここでは偏微分方程式を考えます)が知られていれば,コンピュータを使った計算によってそれに近い現象を再現することができます.そのときの計算方法を考える学問分野を数値解析とよぶことがあります.しかし,数値解析は実在する現象ばかりでなく,自然には起こり得ない現象や容易には観察できない現象を求める手段としても使えます.すなわち,数値解析を用いれば実際には見れない現象を見える化することができます.ここでは,それらの例として,著者らの研究グループで行ってきた形状最適化と逆問題の応用例を紹介したいと思います.それらを通して,数値解析の可能性が広がっていく様子を感じてもらえればと思います.
形状最適化
皆さんにとって身近なランニングシューズをデザインすることを考えてみましょう.オリンピックに出場するような選手ではなく,ときどき健康のためにジョギングするような人のためのシューズを開発することを考えます.そのような人にとって,シューズに求める性能は,脚やひざに過度な負荷がかからないようにするクッション性や正しい姿勢を保持してくれる安定性が大事になります.シューズを設計している人たちがプロネーションとよんでいる現象があります.着地時にかかとが内側に倒れ込む動きです.安定性はこの動きを抑え込む機能であると定義することができます.
私の研究室では,企業の研究者と協力して,このようなクッション性と安定性を両立させるようなソールの形状を求めるための理論と計算方法を開発しました.企業では,ランニング中にシューズにかかる圧力分布の時間変化を計測しています.そのデータを用いれば,クッション性と安定性を特徴づけるそれぞれの姿勢のときの圧力分布が得られます.そのような圧力分布が作用したときのソールの変形は数値解析によって求めることができます.そのような準備ができているもとで,形状最適化問題を次のように考えました.
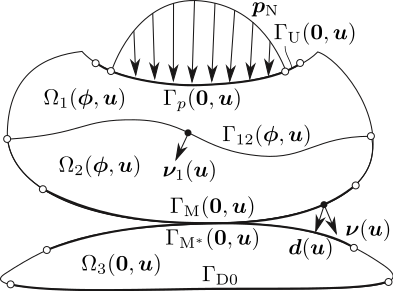
図 1 3つの超弾性体 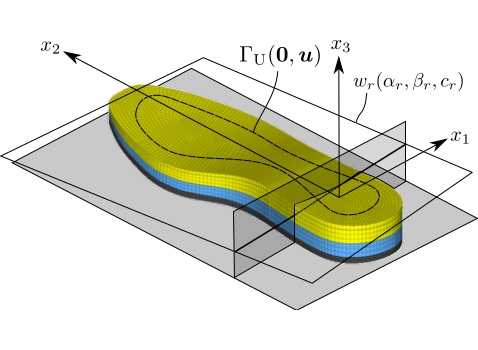
図 2 ソール上面の近似平面
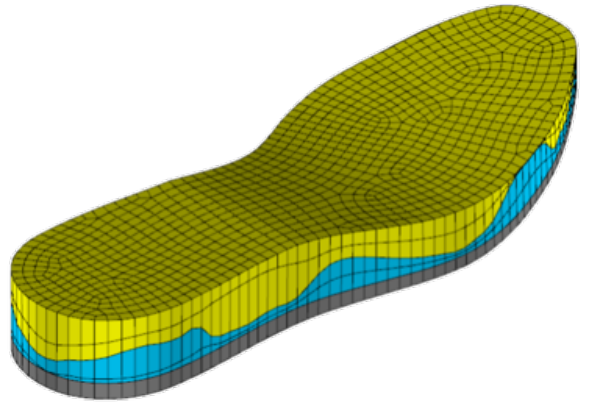
図 3 (a) 最適化されたソール(全体) 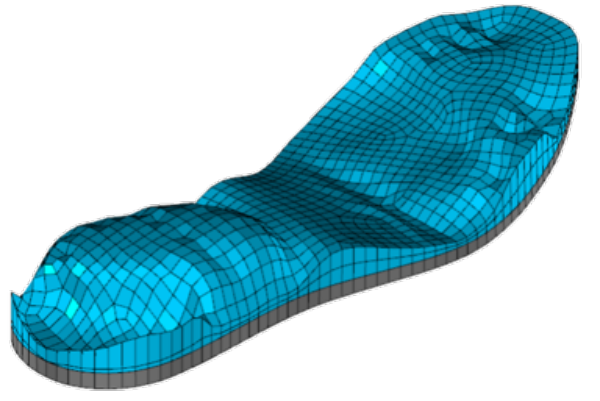
図 3 (b) 最適化されたソール(硬質材)
ソールは,柔らかい材料と硬い材料を貼り合わせてできたゴムのような超弾性体であると仮定します.図 1は理論を考えるために作成した模式図です.一番下の領域の上境界が地面です.ソールはそれに接していて,上部には計測された圧力が作用します.設計したい形状は柔らかい材料と硬い材料の界面です.この研究では,評価関数を次のように選ぶことにしました.図 2 の平面は,圧力を受けて変形したソール上境界の変形を最小二乗法で近似した平面であるとします.クッション性と安定性を評価するそれぞれのタイミングにおけるこの平面の垂直方向の変位と足の幅方向の傾きをクッション性と安定性を表す評価関数とおくことにしました.界面の形状変動に対するこれらの評価関数の変動率は形状微分とよばれ,領域や境界上の関数として定義されます.私の研究室が得意としてきたことは,このような形状微分を計算して,評価関数が減少するような形状変動を求める方法を開発することでした[1,2, 第9章].その方法を用いれば,図 3 のような界面形状が得られます[3].この成果は実際のスポーツシューズ (GEL-KAYANO LITE, ASICS) の設計に活かされています.実際の設計では,界面だけでなく側面も設計対象にされたようです.
逆問題
こんどは,実際にはその現象は存在するのですが,見ることができない現象を見える化する例を紹介したいと思います.この研究は,ある病院の医師らと食品会社の技術者らから相談を受けたことが切っ掛けで始まりました.その研究グループは,嚥下 (食物を飲み込む動作) のメカニズムを数値解析で解明して,誤嚥を起こさないような治療法や食品の開発を目指していました[4].嚥下に関わる各器官の数値モデルは,静止時の CT 画像を用いて作成され,その動きは,実際に水を飲んだ時の X 線画像 (嚥下造影検査) に合わせて,数値モデルを変形させることでつくられました.器官の隙間を水が流れる様子を数値解析で求めていました.この研究グループから受けた相談は,各器官の境界の動きがわかったときに,内部で筋肉が縮む様子を求める (見える化する) ことができますかという内容でした.
この問題は逆問題の用件を満たしています.すなわち,筋肉の動きを表現する数理モデルが与えられたときに,通常は,筋肉の動きを与えて各器官の運動を求めますが,各器官の境界の動きを与えて内部の筋肉の動きを求めるという入出力が逆転した問題になっています.このような問題も,私の研究室で開発してきた密度を設計変数にしたときの位相最適化問題のつくり方 [1,2, 第8章] を応用すれば解けると思われました.密度を筋肉の活動量に置き換えて,観察結果と計算結果のある種の誤差を評価関数におけばよいと考えたわけです.ということで共同研究がスタートしました.
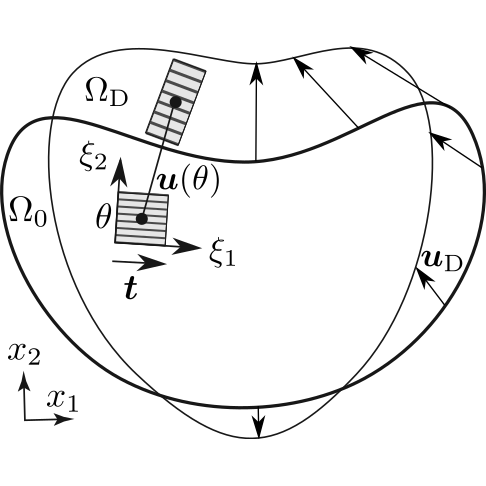
図 4 舌の変形 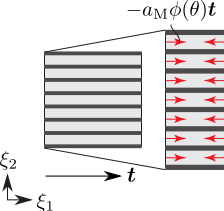
図 5 筋活動 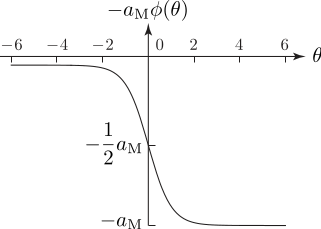
図 6 筋活動の大きさ 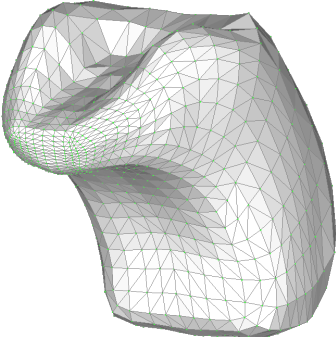
図 7 有限要素モデル 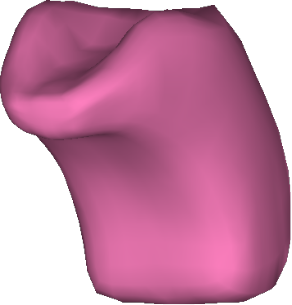
図 8 (a) 形状変化(初期) 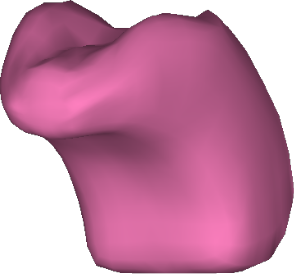
図 8 (b) 形状変化(最終)
その理論を考えたときの模式図を図 4 から 6 に示します.最近になってようやく理論と計算法の成果をまとめることができました[5].共同研究者が作成してくれた図 7 のような舌の数値モデルを使い,図 8 のような舌の動きを入力し,舌を構成する8種類の筋ごとに内部の筋肉が収縮する様子を求めた結果を図 9 に示します.ここで対象にした運動は,水を口に含んで,飲み込み動作を開始した直後 0.27秒間の動きだけを対象にしています.この成果を踏まえて,今後,嚥下に関わる各器官の動きを時間を追って見える化したときに,嚥下のメカニズムが見えてくればこの研究のミッションは達成されたことになります.

図 9 (a) オトガイ舌筋 
図 9 (b) 舌骨舌筋 
図 9 (c) 下縦舌筋 
図 9 (d) 茎突舌筋 
図 9 (e) 上縦舌筋 
図 9 (f) 横舌筋 
図 9 (g) 垂直舌筋 
図 9 (h) 口蓋舌筋
おわりに
この記事では,2つの応用例を通して,私たちの研究によって何ができるようになるのかを紹介しました.しかし,私がやり遂げたいと思っていることは,関数を設計変数とする最適化問題をどのような空間で定義して,どのようにしたら美しく解けるのかを示すことです.それを行うためには,数値解析のほかに,関数解析学とよばれる数学の知識が必要になります.このように,情報学と数学が融合することで,これまで思いもよらなかった見えない現象が数値解析によって見えるようになるかもしれません.
参考文献
[1] 畔上秀幸, 形状最適化問題, 森北出版 (2016).
[2] Azegami, H., Shape optimization problems, Springer (2020). https://doi.org/10.1007/978-981-15-7618-8
[3] Nonogawa, M., Takeuchi, K. and Azegami, H., Shape optimization of running shoes with desired deformation properties, Structural and Multidisciplinary Optimization, Vol. 62, pp. 1535-1546 (2020). https://doi.org/10.1007/s00158-020-02560-0 https://nagoya.repo.nii.ac.jp/record/2001354/files/main.pdf
[4] Kikuchi, T., Michiwaki, Y., Koshizuka, S., Kamiya, T., and Toyama, Y., Numerical simulation of interaction between organs and food bolus during swallowing and aspiration, Computers in Biology and Medicine, Vol. 80, pp. 114-123 (2017). https://doi.org/10.1016/j.compbiomed.2016.11.017
[5] Azegami, H., Ono, S., Takeuchi, K., Kikuchi, T., Michiwaki, Y., Hanyu, K. and Kamiya, T., Identification of muscle activity in tongue motion during swallowing through medical image data, Journal of Biomechanical Science and Engineering, (2021). https://doi.org/10.1299/jbse.21-00254
[6] Ono, S., Azegami, H., Takeuchi, K., Michiwaki, Y. and Kikuchi, T., Identification of muscle activity in tongue’s motion considering distinguished muscle fibers, Proceedings of the Asian Congress of Structural and Multidisciplinary Optimization 2020, p. 159 (2020).

