複雑系科学にノーベル賞!
こんにちは,複雑系科学専攻の時田です。上記のタイトルを見て,「あれ,今年のノーベル物理学賞は温暖化シミュレーションに授与されたのでは?」と思われた方も少なくないかも知れません。確かに,スェーデン王立科学アカデミーのプレスリリース[1]には,
「地球気候を物理的にモデル化し、変動を定量化して地球温暖化の高信頼性予測を可能にした業績」により、半分を真鍋淑郎博士(米国プリンストン大学)とKlaus Hasselmann博士(独マックスプランク研究所)に,そして
「原子スケールから惑星スケールまでの物理系における無秩序とゆらぎの関連の発見」に対して,もう半分をGiorgio Parisi博士(伊ローマ・ラ・サピエンツァ大学)に授与する。
と書かれているのですが,実は,その前に以下のように明記されているのです。
複雑な物理システム(complex physical systems)の理解に画期的な貢献をした業績に対して
つまり,今年のノーベル物理学賞は,複雑系科学の先駆的な研究に対して授与されたとみることができるのです。
名古屋大学にもゆかりのある日本出身の真鍋さんが受賞されたということもあり,メディア各社の報道[2,3]は「温暖化」や「頭脳流出」の問題に集中している印象がありますが,ここでは複雑系科学の観点から,今回受賞されたお三方の研究の歴史的意義や最新研究とのつながりについて学部生や高校生の方にも伝わるように解説してみたいと思います。ブログ記事にしては長い文章になってしまいましたが,最後までお読み頂ければ幸いです。以下真鍋さんを除き人名は論文のスタイルに合わせて敬省略します。
天気予報とカオスの発見
若い方々はあまりピンとこないかも知れませんが,「天気予報は当たらないものだ」と思って育った私と同世代の方々は,「最近は天気予報が当たるようになったなぁ」と感じておられるのではないでしょうか。実は,真鍋さんが研究をされた米国立気象局では,現在スーパーコンピュータをもちいた,全球気象シミュレーションが毎日行われています。日本の気象庁も同様のシミュレーションを行っています。日本の天気予報をするのに,全球,すなわち地球全体の大気や雲の動きを計算しているのです。なので,実は日本の気象庁は米国各地の天気予報もできるし,米国立気象局も日本各地の天気予報ができるので,お互いに「今日はうちの予報の方が当たった」などと予報の正確さを競ったりすることもあるそうです。
真鍋さんが研究を始めた1960年代はコンピューターの性能が十分ではなく,真鍋さんはある一地点の地表から上空までの細長い棒状の空間内での大気や気温の変動をシミュレーションして,二酸化炭素濃度を高く設定すると地表の温度が上がるという「温暖化現象」を世界で初めて発見・予測しました。その先駆的な研究が世界中の気象学者,地球物理学者にも広がり,全球シミュレーションへとつながって,近年の高精度な天気予報に結実しているというわけです。
話はそれますが,皆さんも「ウェザーニュース」という天気予報を行っている会社の名前を目にしたことがあるかと思います。私は昔「気象庁と同じことしてどうやって収益をあげているのだろう?」と不思議に思ったことがあるのですが,実はタンカーや貨物船,漁業関係者などに海の天気情報サービスを提供しているのだそうです。海が荒れると船の燃費が下がり,魚も穫れなくなるので,海の天気予報は経済にも大きな影響を与えます。ここでも,人間が生活している場所以外の海の上の状況まで予測する全球気象シミュレーションが生かされているわけで,真鍋さんの研究の波及効果の大きさがうかがえます。
一方,話を戻すと,1週間程度の短期の天気予報はかなり正確にできるようにはなったのですが,数ヶ月から年といった長期の天気予報は現在でも難しいという状況です。それはなぜなのでしょうか。それには,複雑系科学のキーワードのひとつである「カオス」が深く関係しています。
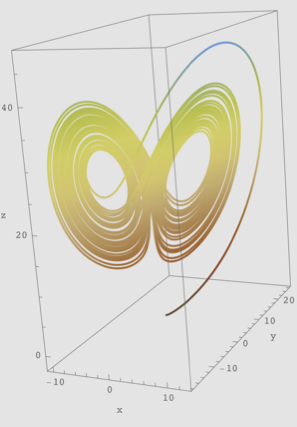
実は,真鍋さんの研究に先駆けて大気の動きをシミュレーションしていた研究者がいました。米国マサチューセッツ工科大学の気象学者Edward Lorenzです。彼は,1960年代初頭にナビエ・ストークス方程式という流体の運動を記述する偏微分方程式から,対流現象を記述する3変数の常微分方程式モデル(ローレンツ方程式)を導きました。それらは非線形の方程式であり解析解が求まらないため,計算機を使ってシミュレーションしてみたところ,確率的な要素のない決定論的方程式なのにも関わらず,初期値に応じて全く異なる複雑な,しかしある種の美しい構造をもつ軌道が現れたのです(図1)。このLorenzによる世界初のカオスの発見により,ローレンツ方程式以外の様々な非線形力学系が示すカオスの研究が爆発的に発展し,現在でもカオスは複雑系科学研究にとってなくてはならない概念となっています。つまり,気象学は複雑系科学の生みの親のひとりといえるわけです。Lorenzは2008年に亡くなってしまったのですが,その前であれば,真鍋さん,Hasselmannと共同受賞していたのではないかとも思われ,複雑系学徒のひとりとしては少し残念な気分でもあります。
Lorenzは1973年に「予測可能性:ブラジルの蝶の羽ばたきがテキサスに竜巻を起こすだろうか?」というタイトルの講演を行いました。また,ローレンツアトラクタ(ローレンツ方程式の軌道の最終的な集合)の特徴的な形状が蝶の羽に似ていることから,「バタフライ効果」はカオスの代名詞になっています。バタフライ効果を生みだすカオスの特徴のひとつに「初期値鋭敏性」があります。カオス系では小さな誤差が指数関数的に増大して,長時間後の軌道を全く予測できなくなってしまうのです。これが長期の天気予報が難しい理由なのですが,これに対してHasselmannは,「気象は変わりやすく,カオスであるにもかかわらず,なぜ気候モデルは信頼できるのか」という疑問に答を出した功績により,真鍋さんと共同受賞となりました。つまり,ある一地点におけるその日その日の雲や風のカオティックな動きを長期予測することは困難でも,年平均気温の長期上昇トレンド,すなわち温暖化現象は十分予測できることを示したわけです。この功績が複雑系科学研究に与えた影響は計り知れないものがあると思われます。「カオスを生み出す複雑系は予測不能なのだから研究しても何の役にも立たないではないか」といった批判に対して,注目する物理量を工夫することにより長期予測が可能となり,政策や経済活動に生かすことができることが示されたからです。気象学は,複雑系科学の生みの親のひとりであるだけでなく,ゆりかごの役割も果たしたといえます。
カオスについては,生態学の方程式にもとづく「ロジスティック写像」の複雑な振る舞いを導入に解説を試みた記事を昔書きました[4]。「高校生にもわかるように」と言われて,数式は最小限におさえたので,興味を持たれた高校生や初学者の方はメールでご請求下さい。
磁石の「出来損ない」が切り開いた新しい世界
誰しも磁石なしの生活をしてきたという人は皆無でしょう。磁石を無効化するテクノロジーを持ったエイリアンが地球にやってきたら,宇宙戦争以前に地球文明は崩壊し,人類は滅びてしまうでしょう。そんな大事な大事な磁石は,皆さんご存知の通り,基本的にはただの鉄の塊です。鉄原子は1個1個が小さな磁石のようなものなのですが,高温のどろどろに溶けた状態では,熱ゆらぎによって個々の鉄原子の磁力の向き(スピン)がばらばらで,全体としてはそれらが相殺してしまい強い磁力が現れません。そのような高温の鉄に外から一方向の磁場をかけながらゆっくりと冷やしていくと,ある温度以下で突然磁力が現れ磁石になるわけです。十分に冷えた磁石はその後再び高温の状態に戻さない限り磁力を失うことはありません。これがあらゆる産業に応用され様々な生活の場面で使われている永久磁石です。
このように,ある温度(もしくは様々な外部のパラメータ)で物質の性質が急激に変化する現象は「相転移」と呼ばれ,昔から,熱力学,統計力学,物性物理学といった分野で研究が重ねられてきました。鉄が示す相転移は「強磁性相転移」と呼ばれており,相転移温度以下の低温では2つの鉄原子の間にはたらく「強磁性相互作用(2つの原子のスピンの向きをそろえようとする力)」が熱ゆらぎに打ち勝つことにより,全ての原子のスピンがそろって全体で磁力を発揮することになるわけです。
強力な磁石の研究開発が進むなかで(富国強兵ならぬ富国強磁性?),1970年代になって,非磁性の金などに鉄を10%以下の低濃度で混ぜて低温にして固めると磁石にならない(のちに)「スピングラス」と呼ばれる物質が発見されました。実は鉄原子間の相互作用は,原子間距離に依存して2つの原子のスピンの向きをそろえようとする力(強磁性相互作用)とそれらの向きを逆転させようとする力(反強磁性相互作用)が混在しており(RKKY相互作用,最後のKは名大の糟谷忠雄のKとYは阪大の芳田奎のY),鉄のみの結晶では全ての原子間距離が一定で強磁性相互作用のみなので磁石になるのですが,スピングラスの場合には,金の中に鉄原子がランダムに散在しているため鉄原子間の距離がばらばらで,それらの間の相互作用も強磁性相互作用と反強磁性相互作用が入り混じったものになっており,そのせいで低温でもスピンがそろわず磁石になりません。スピンがガラスのように無秩序に固まっているので,スピングラスと呼ばれています(グラスもガラスも英語は同じglassなのですが,歴史的事情により無秩序なスピン系はスピン「グラス」と呼ばれています)。
スピングラスは強磁性相転移は起こさないものの,ある温度で比熱がピークを示すなど,何らかの相転移の存在を示唆していました。そこで,スピングラスの統計力学的理論研究を最初に行い,新しい「スピングラス転移」の存在を示したのが,Sam F. Edwardsと1977年にノーベル物理学賞を受賞したPhilip W. Andersonです。Andersonは「量は質を変える(More is different)」という複雑系の本質を見事に表現した有名な言葉を残しています。また,複雑系研究のメッカである米サンタフェ研究所の設立にも関わるなど,「複雑系科学の父」ともいえる存在としても知られています。
さらにその後,全ての鉄原子間の「無限レンジ」相互作用を仮定したハミルトニアン(エネルギー関数)
$$H=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^NJ_{ij}S_iS_j\tag{1}$$
(相互作用\(J_{ij}\)は,対称条件\(J_{ij}=J_{ji}\)を満たす時間的に変動しないランダムなガウス乱数,スピンの向きを表す変数\(S_i\)は,\(S_i=\pm 1\)のように2つの値だけをとる「イジングスピン」,\(N\)は鉄原子の数)を考えるDavid SherringtonとScott Kirkpatrickのモデル(SKモデル)の論文が発表されました。そこでは,EdwardsとAndersonが導入した「レプリカ法」(同じ値のランダム相互作用の組\(\{J_{ij}\}\)を持つ\(N\)個のスピンからなる系の「レプリカ(複製)」を\(n\)個用意して,その全体の自由エネルギーを求める手法)が用いられ,やはりスピングラス転移の存在などが示されたのですが,同時に致命的な問題も見つかりました。SKモデルのエントロピーはモデルの定義上正でなければならないのですが,低温で負になることがわかったのです。
実は,SK論文においては,2つのレプリカ\(\alpha, \beta\)のスピンの向きの「類似度」
$$q_{\alpha\beta}=\frac{1}{N}\sum_{i=1}^NS^{\alpha}_iS^{\beta}_i\tag{2}$$
がレプリカの組み合わせによらず一定値(\(q_{\alpha\beta}=q\))をとるという「レプリカ対称性」を仮定し,「レプリカ対称解」を求めていたのですが,J.R.L. de AlmeidaとDavid. J. Thouless(2016年ノーベル物理学賞受賞)が,レプリカ対称解はスピングラス転移温度以下の低温領域(スピングラス相)で不安定であり,スピングラス相を正しく表していないという驚くべき結果を発表したのです。
「レプリカ対称性が現実にはありえない」ということは,今から考えれば当然のことと感じられます。鉄原子間には強磁性相互作用と反強磁性相互作用が入り混じっているので,統計的には鉄原子のスピンは半分が上向き(\(S_i=+1\)),半分が下向き(\(S_i=-1\))になり全体としては磁力が相殺され磁石にならないわけですが,そのような状況を実現するスピンの向きの上下の組み合わせはレプリカごとに多様ですから,レプリカ間の類似度((2)式)が全て同じ値になる(レプリカ対称性)ということは直感的にもありえないのです。
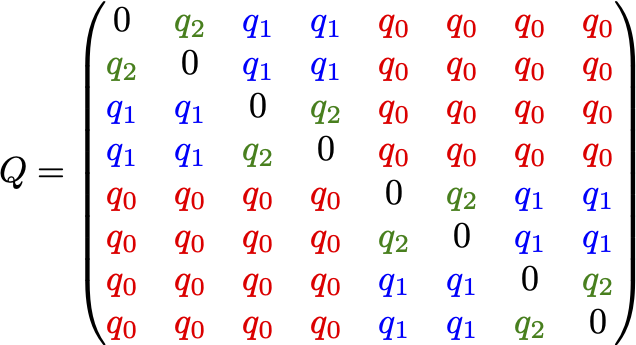
そこで,「レプリカ対称性の破れ(Replica Symmetry Breaking)」と,スピングラス相でも安定な「RSB解」もしくは「パリシ解」を発見したのが,今回ノーベル物理学賞の半分を受賞した伊ローマ・サピエンツァ大学のGiorgio Parisiです。
パリシ解(パリシ行列)を四半世紀ぶりに書いてみました(図2)。実は,私は昔大学院生のときに,ニューラルネットワーク(Hopfieldモデル)のパリシ解を求めたことがあり,博士論文の中にもこのパリシ行列を書いていたのです(当時はパリシ解にノーベル賞が出るとは夢にも思わず!)。図2のパリシ行列はレプリカ対称性が2回破れた状況を表しており,類似度は\(q_{\alpha\beta}=q_0, q_1, q_2\)の3種類の値を取っています(同一レプリカ間の類似度は定義上\(q_{\alpha\alpha}=1\)ですがここでは0にしてあります)が,SKモデルの場合は,レプリカ対称性が無限回破れており,パリシ行列は\(\infty\times\infty\)の行列になります。スピングラス,すなわち磁石の「出来損ない」は,レプリカひとつの中のスピンの並びを見ると無秩序に見えるのですが,2つのレプリカの類似度((2)式)に注目すると,低温で(熱ゆらぎが弱まると)図2のような美しい階層構造が出現するわけです。これが,受賞理由の「物理系における無秩序とゆらぎの関連」です。
これだけでも十分驚きなのですが,その後,AIや機械学習の分野で使われているニューラルネットワークや,符号器などの様々な情報システム,巡回セールスマン問題やSATなどの組合せ最適化問題((1)式のエネルギー関数を最小化する\(S_i\)の値の探索は,NP困難問題であることが示されています),さらには生態系,遺伝子ネットワーク,病原体と免疫系のネットワークなどの様々な複雑系においてレプリカ対称性の破れが発見されて,世の中の無秩序に見える「モノ」や「コト」の背後に共通の隠された秩序があることがわかってきたのです。そのような,複雑な世界に対する新しい理解の仕方を見つけたことに対して,ノーベル賞が授与されたということです。

左の写真は最近の私のラボでのゼミ風景です。ノーベル賞が出たからあわてて勉強しているというわけではありません。今年の4月から,この分野の定番である教科書「スピングラス理論と情報統計力学[5]」のゼミをしてきたのですが,先週はちょうどレプリカ対称性の破れやパリシ解のところにさしかかったので,学生さんたちの了承を得たうえでシェアします。私のラボの大学院生は,進化ダイナミクス,言語進化モデル,さらには深層学習ニューラルネットワークにおけるレプリカ対称性の破れを研究しています。
このように,今回のノーベル賞受賞者たちが発見・開拓した,カオスやレプリカ対称性の破れといった概念は,決して終了した学問の主題ではなく,現在でも最新の複雑系研究にとってなくてはならないものとなっています。複雑系科学専攻に所属して,複雑系の探求を続ける一学徒として,心から今回のノーベル賞をお祝いしたいと思います。
本稿を最後まで読んでくださりありがとうございました。複雑系研究に興味を持たれた高校生や学部生の方は,ぜひ名古屋大学情報学部,大学院情報学研究科複雑系科学専攻への進学をご検討ください。
- Press release: The Nobel Prize in Physics 2021, https://www.nobelprize.org/prizes/physics/2021/press-release/ (参照2021年10月10日)
- 真鍋さんノーベル賞、ゆかりの名大でも祝福「非常に励みになる」,毎日新聞,10月5日,https://mainichi.jp/articles/20211005/k00/00m/040/333000c (参照2021年10月10日)
- ノーベル物理学賞受賞・真鍋淑郎さん 名古屋の思い出を語る, 中日新聞,10月5日,https://www.chunichi.co.jp/article/342540 (参照2021年10月10日)
- 時田恵一郎,「蝶の羽ばたきは嵐を呼ぶか?:カオスは生命をかく語りき」,細胞工学,Vol.23, No.9, 2004, pp.1070-1076.
- 西森秀稔,「スピングラス理論と情報統計力学」,岩波書店,1999年.
時田 恵一郎
名古屋大学 大学院情報学研究科 複雑系科学専攻 教授
専門は複雑系科学,統計力学、数理生物学、多様性の科学

